The Degree Diameter Problem for General Mixed Graphs

Introduction

The degree/diameter problem for general mixed graphs can be stated as follows:

Given three natural numbers [math]r[/math], [math]z[/math] and [math]k[/math], find the largest possible number [math]N(r,z,k)[/math] of vertices in a mixed graph of maximum undirected degree [math]r[/math], maximum directed out-degree [math]z[/math] and diameter [math]k[/math].

In attempting to settle the values of [math]N(r,z,k)[/math], research activities in this problem have follow the following two directions:

• Increasing the lower bounds for [math]N(r,z,k)[/math] by constructing ever larger mixed graphs.

• Lowering and/or setting upper bounds for [math]N(r,z,k)[/math] by proving the non-existence of mixed graphs

whose order is close to the Moore bound [math]M(r,z,k)=A(u^{k+1}-1)(u-1)^{-1}+B(w^{k+1}-1)(w-1)^{-1} [/math], where [math]v=(z+r)^2+2(z-r)+1[/math], [math]u=(1/2)(z+r-1-v^{1/2})[/math], [math]w=(1/2)(z+r-1+v^{1/2})[/math], [math]A=(v^{1/2}-(z+r+1))(2v^{1/2})^{-1}[/math] and [math]B=(v^{1/2}+(z+r+1))(2v^{1/2})^{-1}[/math].

Mixed Moore graphs

Mixed graphs of order [math]M(r,z,k)[/math] with maximum undirected degree [math]r[/math], maximum directed out-degree [math]z[/math] and diameter [math]k[/math] are called mixed Moore graphs. Such extremal mixed graphs are totally regular of degree [math]d=r+z[/math] and they have the property that for any ordered pair [math](u,v)[/math] of vertices there is a unique trail from [math]u[/math] to [math]v[/math] of length at most the (finite) diameter [math]k[/math]. It is proved that mixed Moore graphs may only exist for diameter [math]k=2[/math]. In this case, Bosák gives the following necessary condition for their existence:

Let [math]G[/math] be a (proper) mixed Moore graph of diameter 2. Then, [math]G[/math] is totally regular with directed degree [math]z\gt 0[/math] and undirected degree [math]r\gt 0[/math]. Moreover, there must exist a positive odd integer [math]c[/math] such that [math]r = (1/4)(c^2+3)[/math] and [math]c | (4z-3)(4z+5)[/math].

As a consequence, these extremal graphs may only exist for some (infinitely many) values of the order [math]n[/math]. Nevertheless, the existence of these graphs have been proved only for a 'few' cases. The unique infinite family of mixed Moore graphs known is the Kautz digraphs [math]Ka(1+z,2)[/math], for every [math]z\gt 1[/math] and [math]r=1[/math] (where every digon has been identified by an edge). Gimbert proved that Kautz digraphs are the unique mixed Moore graphs with those parameters. An interesting proper mixed Moore graph of order 18 was given by Bosák (and its uniqueness was proved later by Nguyen et al.).

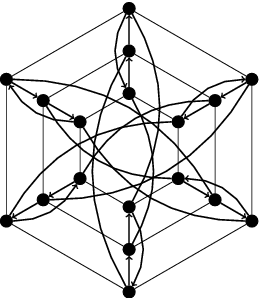
Jorgensen found two non-isomorphic proper mixed Moore graphs of order 108 of Cayley type. Recently, López et al. prove the non existence of mixed Moore graphs of orders 40, 54 and 84, translating the existence of the adjacency matrix of these mixed graphs through the Boolean satisfiability problem. Besides, there are many pairs [math](r,z)[/math] satisfying Bosák necessary condition for which the existence of a proper mixed Moore graph was not yet known until now:

[math]M(r,z,2)[/math]	[math]r[/math]	[math]z[/math]	[math]d[/math]	Existence	Uniqueness
6	1	1	2	ka(2,2)	Yes
12	1	2	3	ka(3,2)	Yes
18	3	1	4	Bosák graph	Yes
20	1	3	4	ka(4,2)	Yes
30	1	4	5	ka(5,2)	Yes
40	3	3	6	No	-
42	1	5	6	ka(6,2)	Yes
54	3	4	7	No	-
56	1	6	7	ka(7,2)	Yes
72	1	7	8	ka(8,2)	Yes
84	7	2	9	No	-
88	3	6	9	Unknown	Unknown
90	1	8	9	ka(9,2)	Yes
108	3	7	10	Jorgensen graphs	No
110	1	9	10	ka(10,2)	Yes
132	1	10	11	ka(11,2)	Yes
150	7	5	12	Unknown	Unknown
154	3	9	12	Unknown	Unknown
156	1	11	12	ka(12,2)	Yes
180	3	10	13	Unknown	Unknown
182	1	12	13	ka(13,2)	Yes

IN PREPARATION